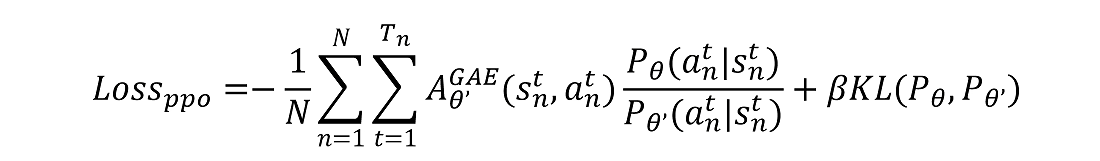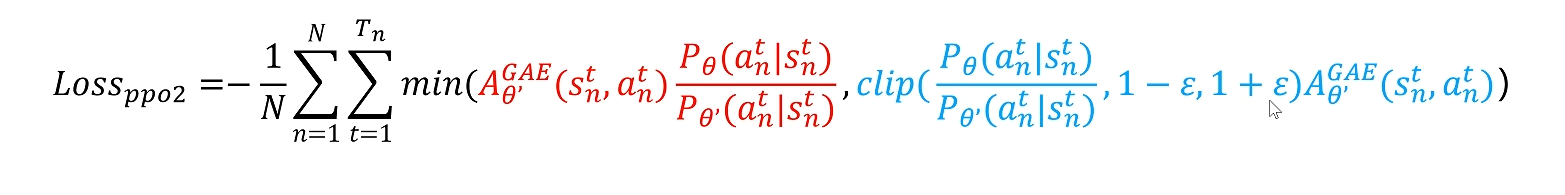前提
这段时间参加比赛需要利用到强化学习,但是强化学习中的概念和名词非常的多,再加上本人比较菜,容易混淆概念,故写篇博客来辅助学习。由于是学习时候遇到的不理解的内容,故可能结构比较松散。
(博客的公式好像有大问题,但是 markdown 显示没啥问题,好奇怪,估计是下载成 katex 了,算了,先学东西吧,后面再挑)
强化学习的基本思想
强化学习(reinforcement learning,RL)讨论的问题是智能体(agent)怎么在复杂、不确定的环境(environment)里面去最大化它能获得的奖励。
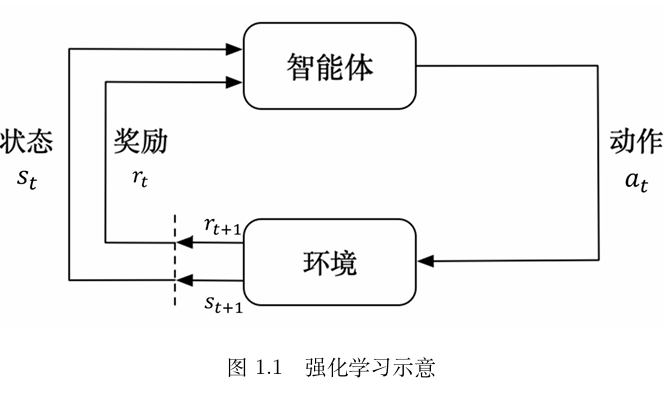
如图,强化学习由两部分组成:智能体和环境 。在强化学习过程中,智能体与环境一直在交互。智能体在环境里面获取某个状态后,它会利用该状态输出一个动作(action),这个动作也称为决策(decision)。然后这个动作会在环境之中被执行,环境会根据智能体采取的动作,输出下一个状态以及当前这个动作带来的奖励。智能体的目的就是尽可能多地从环境中获取奖励 。
简单来说就是利用算法,使得智能体可以适应环境完成相应的任务。
相关概念
基础概念
reward
奖励是在某个时间步上由环境给予智能体(Agent)的反馈信号,用以表明智能体在当前状态下采取某个动作的好坏。
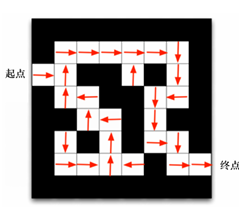
以走迷宫为例子来讲解 reward ,比如说在此迷宫中怎么评价智能体是否走对了?
我们规定,智能体往正确的方向行走,那么我们给这一步规定为 1 ,反之走错则为 -1,那么这个 1 与 -1 就是每一步的 reward
return
回报是从当前时间步开始,智能体在未来一系列时间步内所能获得的奖励的总和,通常这个总和会被一个折扣因子(Discount Factor)所折扣,以体现未来奖励的不确定性或时间价值。
用公式表示就是:
r e t u r n = ∑ k = 0 ∞ γ k R r + k + 1 return = \sum_{k=0}^\infty \gamma ^ k R_{r+k+1}
r e t u r n = k = 0 ∑ ∞ γ k R r + k + 1
即从当前状态开始考虑未来一系列动作所能获得的累积奖励
Trajectory
将当前的智能体与环境交互,会得到一系列观测。每一个观测可看成一个轨迹(trajectory)。轨迹就是当前帧以及它采取的策略,即状态和动作的序列:
episode
当在某一个 policy 下,Agent 可能在某个状态停止执行,那么这个特殊的 trajectory 就称为 episode ,即一次尝试。(就是一局游戏)
DQN
之后有空了再写…
PPO
关于 PPO 算法证明我主要是参考的参考文章 3 的内容,然后加上些自己的理解,证明思路也是小标题顺序。呃呃呃,大家凑合着看吧。
参考文章
https://blog.csdn.net/weixin_41106546/article/details/137359690 https://www.jianshu.com/p/8803cb2d4e30 【零基础学习强化学习算法:ppo】https://www.bilibili.com/video/BV1iz421h7gb?vd_source=cb24236e5cb2727cf94bda12dc00cd9b (真的很推荐去看下)
相关论文: https://arxiv.org/abs/1707.06347
开源代码: https://github.com/openai/baselines
Policy Gradient(PG)
PG的主要思想是在 π ( a ∣ s , θ ) \pi(a|s, \theta) π ( a ∣ s , θ )
详细步骤
相关定义 : 首先,定义一个参数化的策略 π ( a ∣ s , θ ) π(a∣s,θ) π ( a ∣ s , θ ) 样本采集 :使用当前策略 π ( a ∣ s , θ ) π(a∣s,θ) π ( a ∣ s , θ ) ( s , a , r ) (s,a,r) ( s , a , r ) 计算回报 :对于每个样本,计算从该样本开始到轨迹结束的累计回报(return),这通常是通过某种形式的回报折扣(如时间差分学习中的回报)来计算的。梯度估计 :根据采集到的样本和计算出的回报,估计策略梯度 ∇ θ J ( θ ) ∇_θJ(θ) ∇ θ J ( θ ) 策略更新:使用梯度上升方法更新策略参数 θ,以增加导致高回报的行动的概率,减少导致低回报的行动的概率。
相关公式推导(非严谨)
我们主要是想要得到一个最优的 π \pi π r e t u r n return r e t u r n θ \theta θ θ \theta θ θ \theta θ
E ( x ) x − p ( x ) = 1 N ∑ i = 1 N x E(x)_{x-p(x)} = \frac{1}{N}\sum_{i=1}^N{x}
E ( x ) x − p ( x ) = N 1 i = 1 ∑ N x
对前面两项进行近似期望,后面利用 l o g log l o g
tips 1 加入折扣因子 γ \gamma γ
由于每一步不是对后面所有的步数都有所影响,可能只会影响到后面的几步,因此加入折扣因子 γ \gamma γ
tips 2 加入baseline
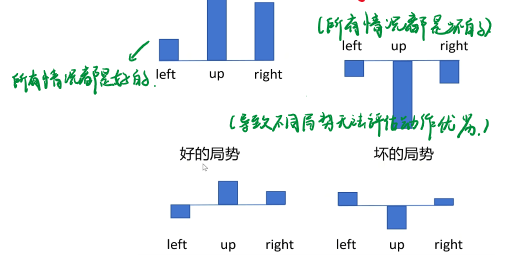
考虑存在以下两种情况:
1.在局势十分好的情况,采集到的样本得到的 r e t u r n return r e t u r n r e t u r n return r e t u r n
这样训练会影响模型的稳定性
因此我们加入一个baseline,对每个值进行相减,得到的是有正有负的概率分布
B ( S n t ) B(S_n^t) B ( S n t )
GAE
参考
这篇文章也是讲的很清晰
1 https://zhuanlan.zhihu.com/p/549145459
GAE 的主要思想是想解决单步采样与多步采样之间方差与偏差的关系,即
单步采样的方差小,偏差大;多步采样的方差大,但偏差小(大概是机器学习的内容)
那么我们将全部的采样都加入到一个式子中,并引入对应的权重 γ \gamma γ
重要性采样
重要性采样主要在叙述什么事情嘞,其实很简单,就是想要将一个空间上面的采样映射到另一个空间上。
散度
为什么会引入这个概念呢,就是因为可能存在有 两个空间的差别太大导致的相关问题 ,因此我们引入散度加以限制
下面的 PPO 与 PPO2 之间的主要差别也是很明显的 —— 约束的方式不同,通过不同的约束条件来优化差别,也就不仔细讲解了
PPO
PPO2
实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 import numpy as npimport torchfrom torch import nnfrom torch.nn import functional as Fclass PolicyNet (nn.Module): def __init__ (self, n_states, n_hiddens, n_actions ): super (PolicyNet, self ).__init__() self .fc1 = nn.Linear(n_states, n_hiddens) self .fc2 = nn.Linear(n_hiddens, n_actions) def forward (self, x ): x = self .fc1(x) x = F.relu(x) x = self .fc2(x) x = F.softmax(x, dim=1 ) return x class ValueNet (nn.Module): def __init__ (self, n_states, n_hiddens ): super (ValueNet, self ).__init__() self .fc1 = nn.Linear(n_states, n_hiddens) self .fc2 = nn.Linear(n_hiddens, 1 ) def forward (self, x ): x = self .fc1(x) x = F.relu(x) x = self .fc2(x) return x class PPO : def __init__ (self, n_states, n_hiddens, n_actions, actor_lr, critic_lr, lmbda, epochs, eps, gamma, device ): self .actor = PolicyNet(n_states, n_hiddens, n_actions).to(device) self .critic = ValueNet(n_states, n_hiddens).to(device) self .actor_optimizer = torch.optim.Adam(self .actor.parameters(), lr=actor_lr) self .critic_optimizer = torch.optim.Adam(self .critic.parameters(), lr=critic_lr) self .gamma = gamma self .lmbda = lmbda self .epochs = epochs self .eps = eps self .device = device def take_action (self, state ): state = torch.tensor(state[np.newaxis, :]).to(self .device) probs = self .actor(state) action_list = torch.distributions.Categorical(probs) action = action_list.sample().item() return action def learn (self, transition_dict ): states = torch.tensor(transition_dict['states' ], dtype=torch.float ).to(self .device) actions = torch.tensor(transition_dict['actions' ]).to(self .device).view(-1 , 1 ) rewards = torch.tensor(transition_dict['rewards' ], dtype=torch.float ).to(self .device).view(-1 , 1 ) next_states = torch.tensor(transition_dict['next_states' ], dtype=torch.float ).to(self .device) dones = torch.tensor(transition_dict['dones' ], dtype=torch.float ).to(self .device).view(-1 , 1 ) next_q_target = self .critic(next_states) td_target = rewards + self .gamma * next_q_target * (1 - dones) td_value = self .critic(states) td_delta = td_target - td_value td_delta = td_delta.cpu().detach().numpy() advantage = 0 advantage_list = [] for delta in td_delta[::-1 ]: advantage = self .gamma * self .lmbda * advantage + delta advantage_list.append(advantage) advantage_list.reverse() advantage = torch.tensor(advantage_list, dtype=torch.float ).to(self .device) old_log_probs = torch.log(self .actor(states).gather(1 , actions)).detach() for _ in range (self .epochs): log_probs = torch.log(self .actor(states).gather(1 , actions)) ratio = torch.exp(log_probs - old_log_probs) surr1 = ratio * advantage surr2 = torch.clamp(ratio, 1 - self .eps, 1 + self .eps) * advantage actor_loss = torch.mean(-torch.min (surr1, surr2)) critic_loss = torch.mean(F.mse_loss(self .critic(states), td_target.detach())) self .actor_optimizer.zero_grad() self .critic_optimizer.zero_grad() actor_loss.backward() critic_loss.backward() self .actor_optimizer.step() self .critic_optimizer.step() import numpy as npimport matplotlib.pyplot as pltimport gymnasium as gymimport torchdevice = torch.device('cuda' ) if torch.cuda.is_available() \ else torch.device('cpu' ) num_episodes = 100 gamma = 0.9 actor_lr = 1e-3 critic_lr = 1e-2 n_hiddens = 16 env_name = 'CartPole-v1' return_list = [] env = gym.make(env_name, render_mode="human" ) n_states = env.observation_space.shape[0 ] n_actions = env.action_space.n agent = PPO(n_states=n_states, n_hiddens=n_hiddens, n_actions=n_actions, actor_lr=actor_lr, critic_lr=critic_lr, lmbda=0.95 , epochs=10 , eps=0.2 , gamma=gamma, device=device ) for i in range (num_episodes): state = env.reset()[0 ] done = False episode_return = 0 transition_dict = { 'states' : [], 'actions' : [], 'next_states' : [], 'rewards' : [], 'dones' : [], } while not done: action = agent.take_action(state) next_state, reward, done, _, _ = env.step(action) transition_dict['states' ].append(state) transition_dict['actions' ].append(action) transition_dict['next_states' ].append(next_state) transition_dict['rewards' ].append(reward) transition_dict['dones' ].append(done) state = next_state episode_return += reward return_list.append(episode_return) agent.learn(transition_dict) print (f'iter:{i} , return:{np.mean(return_list[-10 :])} ' ) plt.plot(return_list) plt.title('return' ) plt.show()
备注
为什么 PPO 没有经验回访池
重要性采样的前提要求:相关的空间转化是不能够差别太大
名词区分
return && reward
reward 是环境对智能体单个动作的反馈。而 return 是从当前状态开始考虑未来一系列动作所能获得的累积奖励。强化学习的目标是找到一个策略来最大化期望的 return 。
On-policy && Off-policy
On-policy 学习是智能体通过当前策略与环境交互并自主更新策略的过程,而 Off-policy 学习则允许智能体通过不同的行为策略进行经验积累,并更新不同的目标策略。
其实主要区别就是看 数据采样 与 模型学习 是否是一样的网络
举例来说:On-policy ), 其他同学在旁边看着老师教育小明明白上课不能睡觉( Off-policy )
参考
1 https://zhuanlan.zhihu.com/p/346433931
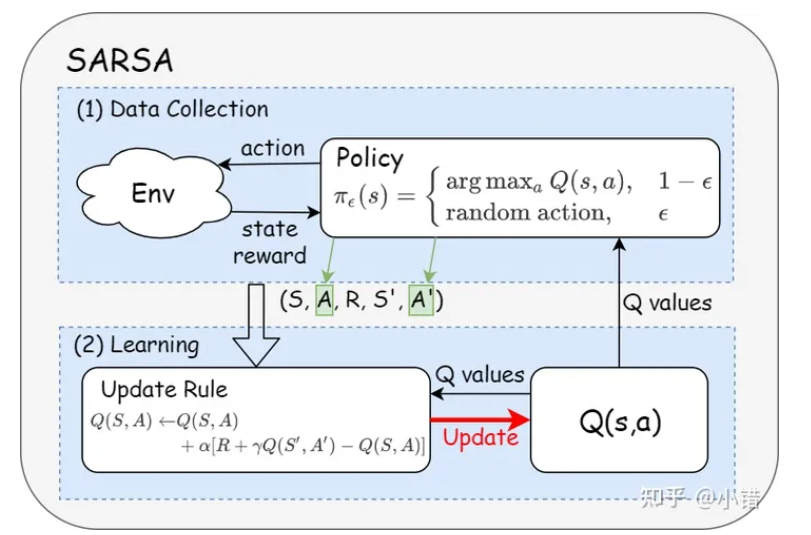
On-policy
On-policy 学习: 在 On-policy 学习中,智能体根据当前策略来进行学习和更新。这意味着智能体在与环境交互时,基于当前策略选择动作,并使用这些动作的结果来更新该策略。经典的 On-policy 算法包括 SARSA (State-Action-Reward-State-Action)。
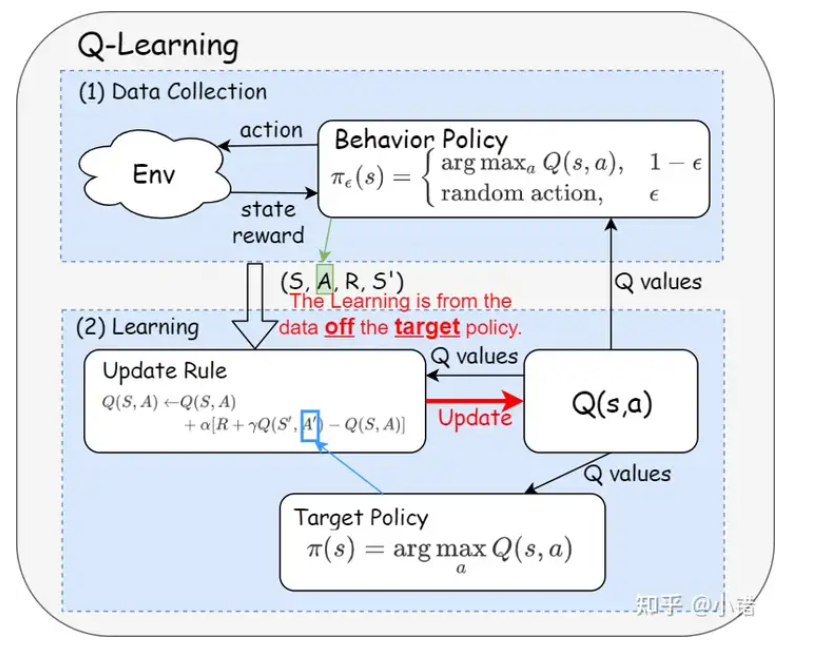
off-policy
Off-policy 学习: 在 Off-policy 学习中,智能体使用一种行为策略(behavior policy)来与环境交互,但学习和更新的策略可以不同(目标策略,target policy)。这允许智能体从不同于当前策略的经验中学习。一个典型的 Off-policy 算法是 Q-learning,它通过与环境交互(可能是随机或基于某种行为策略),但更新的是贪心策略(目标策略)。